Answer:
99.7% of the confidence intervals we could construct after repeated sampling would go from 12.64 cm to 14.44 cm.
True that's the correct interpretation for this case since if we repeat the measures with this sample size we will got a similar result.
Explanation:
For this case we need to remember that the confidence interval for the true mean is given by this formula:
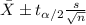
And for this case the 99.7 % confidence interval for the true mean is (12.64cm , 14.44cm) we analyze one by one the possible options in order to select one:
99.7% of the confidence intervals we could construct after repeated sampling would go from 12.64 cm to 14.44 cm.
True that's the correct interpretation for this case since if we repeat the measures with this sample size we will got a similar result.
There's a 99.7% chance that any particular frog I catch can jump between 12.64 cm and 14.44 cm.
False the confidence interval can't be interpreted as a chance
There's a 99.7% chance that the the mean length of frog jumps falls between 12.64 cm and 14.44 cm.
False the confidence interval can't be interpreted as a chance
If we were to repeat this sampling many times, 99.7% of the confidence intervals we could construct would contain the true population mean.
False always the confidence interval contain the mean since is the middle value.