Question

1 point) The physical fitness of an athlete is often measured by how much oxygen the athlete takes in (which is recorded in milliliters per kilogram, ml/kg). The mean maximum oxygen uptake for elite athletes has been found to be 65 with a standard deviation of 5.3. Assume that the distribution is approximately normal. (a) What is the probability that an elite athlete has a maximum oxygen uptake of at least 50 ml/kg

Answer 1

The probability that an elite athlete has a maximum oxygen uptake of at least 50 ml/kg is 0.9970.

Explanation:

The random variable X can be defined as the amount of oxygen an athlete takes in.

The mean maximum oxygen uptake for elite athletes is, μ = 65 ml/kg.

The standard deviation is, σ = 5.3 ml/kg.

The random variable X is approximately normally distributed.

Now to compute probabilities of a normally distributed random variable, we first need to convert the value of X to a z-score.

`z=(x-\mu)/(\sigma)`

The distribution of these z-scores is known as a Standard normal distribution, i.e.
`Z\sim N(0, 1)`.

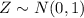A normal distribution is a continuous distribution. So, the probability at a point on a normal curve is 0. To compute the exact probabilities we need to apply continuity correction.

Compute the probability that an elite athlete has a maximum oxygen uptake of at least 50 ml/kg as follows:

P (X ≥ 50) = P (X > 50 + 0.50)

= P (X > 50.50)

`=P((x-\mu)/(\sigma)>(50.50-65)/(5.3))`

`=P(Z>-2.74)\\=P(Z<2.74)\\=0.99693\\\approx 0.9970`

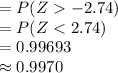
Thus, the probability that an elite athlete has a maximum oxygen uptake of at least 50 ml/kg is 0.9970.