Question

An airplane is traveling at 150 m/s in level flight. In order to make a change in direction, the airplane travels in a horizontal curved path. To fly in the curved path, the pilot banks the airplane at an angle such that the lift has a horizontal component that provides the horizontal radial acceleration to move in a horizontal circular path. If the airplane is banked at an angle of 12.0 degrees, then the radius of curvature of the curved path of the airplane is

Answer 1

Given Information:

Velocity = v = 150 m/s

angle = θ = 12°

Required Information:

Radius of curvature = R = ?

Answer:

Radius of curvature =
`R = 1.079 * 10^(4) \: m`

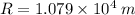
Step-by-step explanation:

Please refer to the attached diagram,

`Fcos(\theta) = m \cdot g\\Fcos(12^(\circ)) = m \cdot g \:\:\:\:\:\:eq. 1`

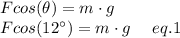
Where m is the mass of the plane and g is the gravitational acceleration.

`Fsin(\theta) = (mv^(2))/(R)\\Fsin(12^(\circ)) = (m \cdot v^(2))/(R)\:\:\:\:\:\:eq. 2`

Where v is the velocity of the plane and R is the radius of curvature of the curved path of the airplane.

Dividing eq. 2 by eq. 1 yields,

`tan(12^(\circ)) = (v^(2))/(R\cdot g )`

`since \: (sin(\theta))/(cos(\theta)) = tan(\theta)`

`tan(12^(\circ)) = (v^(2))/(R\cdot g )\\\\R = (v^(2))/(g\cdot tan(12^(\circ)) )\\\\R = (150^(2))/(9.81\cdot 0.212 )\\\\R = 10793\\R = 1.079 * 10^(4) \: m`

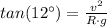
Therefore, the radius of curvature of the curved path of the airplane is 1.079×10⁴ m