Answer:
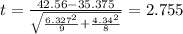
The degrees of freedom are given by:
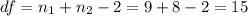
Since we have a two tailed test the p value can be calculated like this:
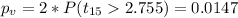
And since the p value is lower than the significance lvel given of 0.05 we have enough evidence to conclude that we have significant differences between the two groups on this case.
Explanation:
We have the following data given:
Business Travelers
42 31 37 45 49 52 43 39 45
Leisure Travelers
32 29 35 40 38 34 42 33
For this case we need to begin finding the sample mean and deviations for each group with the following formulas:

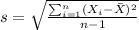
And we got:
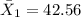 represent the sample mean for the Business travelers
represent the sample mean for the Business travelers
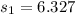 represent the sample deviation for the Business travelers
represent the sample deviation for the Business travelers
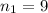 the sample size for the Business travelers
the sample size for the Business travelers
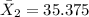 represent the sample mean for the Leisure travelers
represent the sample mean for the Leisure travelers
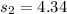 represent the sample deviation for the Leisure travelers
represent the sample deviation for the Leisure travelers
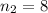 the sample size for the Leisure travelers
the sample size for the Leisure travelers
The system of hypothesis for this case are:
Null hypothesis:

Alternative hypothesis:
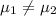
The statistic for this case is given by:
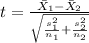
And replacing we got:
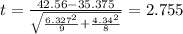
The degrees of freedom are given by:
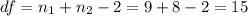
Since we have a two tailed test the p value can be calculated like this:
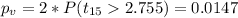
And since the p value is lower than the significance lvel given of 0.05 we have enough evidence to conclude that we have significant differences between the two groups on this case.