Question

A person recently read that 84% of cat owners are women. How large a sample should the researcher take if she wishes to be 90% confident that her proportion is within 3% of the true population proportion?

Answer 1

405

Explanation:

To find sample size, use the following equation, where n = sample size, za/2 = the critical value, p = probability of success, q = probability of failure, and E = margin of error.

`n=\frac{(z_{(\alpha )/(2) })^(2) *p*q }{E^2}`

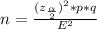
The values that are given are p = 0.84 and E = 0.03.

You can solve for the critical value which is equal to the z-score of (1 - confidence level)/2. Use the calculator function of invNorm to find the z-score. The value will given with a negative sign, but you can ignore that.

(1 - 0.9) = 0.1/2 = 0.05

invNorm(0.05, 0, 1) = 1.645

You can also solve for q which is 1 - p. For this problem q = 1 - 0.84 = 0.16

Plug the values into the equation and solve for n.

`n =((1.645)^2*0.84*0.16)/((0.03)^2)\\n= 404.0997333`

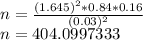
Round up to the next number, giving you 405.