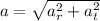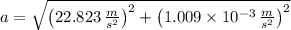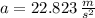Answer:
a)
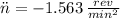 , b)
, b)
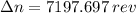 , c)
, c)
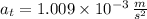 , d)
, d)
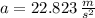
Step-by-step explanation:
a) Constant angular acceleration is:
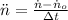
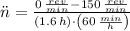
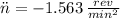
b) The amount of revolutions required to stop the flywheel is:
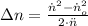
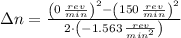
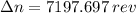
c) The tangential acceleration of the particle is:

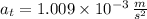
d) The radial acceleration of the particle is:
![a_(r) = \left[\left(75\,(rev)/(min) \right)\cdot \left((1)/(60)\,(min)/(s) \right)\cdot \left(2\pi\,(rad)/(rev) \right)\right]^(2)\cdot (0.37\,m)](https://img.qammunity.org/2021/formulas/physics/college/74vq69cxflbupl4lt1bne3byfoq6o8tq1y.png)

The net linear acceleration is: