Question

A facilities manager at a university reads in a research report that the mean amount of time spent in the shower by an adult is 5 minutes. He decides to collect data to see if the mean amount of time that college students spend in the shower is significantly different from 5 minutes. In a sample of 15 students, he found the average time was 4.29 minutes and the standard deviation was 0.75 minutes. Using this sample information, conduct the appropriate hypothesis test at the 0.01 level of significance. Assume normality.a) What are the appropriate null and alternative hypotheses?H0: ? = 5 versus Ha: ? ? 5H0: x = 5 versus Ha: x ? 5 H0: ? = 5 versus Ha: ? < 5H0: ? = 5 versus Ha: ? > 5b) What is the test statistic? Give your answer to four decimal places. c) What is the P-value for the test? Give your answer to four decimal places. d) What is the appropriate conclusion?

Answer 1

(a) H₀: μ = 5 vs. Hₐ: μ ≠ 5.

(b) The test statistic value is -3.67.

(c) The p-value of the test is 0.0025.

(d) The mean amount of time spent in the shower by an adult is different from 5 minutes.

Explanation:

In this case we need to test whether the mean amount of time that college students spend in the shower is significantly different from 5 minutes.

The information provided is:

`n=15\\\bar x=4.29\\s=0.75\\\alpha =0.01`

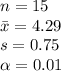
(a)

The hypothesis for the test can be defined as follows:

H₀: The mean amount of time spent in the shower by an adult is 5 minutes, i.e. μ = 5.

Hₐ: The mean amount of time spent in the shower by an adult is different from 5 minutes, i.e. μ ≠ 5.

(b)

As the population standard deviation is not known we will use a t-test for single mean.

Compute the test statistic value as follows:

`t=(\bar x-\mu)/(s/√(n))\\\\=(4.29-5)/(0.75/√(15))\\\\=-3.67`

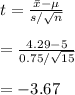
Thus, the test statistic value is -3.67.

(c)

Compute the p-value of the test as follows:

`p-value=2* P(t_(\alpha/2, (n-1))<-3.67)\\ =2* P(t_(0.005, 14)<-3.67)\\=0.0025`

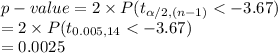
*Use a t-table.

Thus, the p-value of the test is 0.0025.

(d)

Decision rule:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.

p-value = 0.0025 < α = 0.01

The null hypothesis will be rejected at 1% level of significance.

Thus, concluding that the mean amount of time spent in the shower by an adult is different from 5 minutes.