Question

Martha, A statistician wishes to analyze teachers’ salaries in the state of California. She determines that teacher’s salaries in California are normally distributed with a mean salary of $37,764 and a standard deviation of $5,100. Answer the following questions. a) What is the probability that a randomly selected teacher’s salary in California is greater than $45,000?

Answer 1

0.078 or 7.8%

Explanation:

Mean salary (μ) = $37,764

Standard deviation (σ) = $5,100

The z-score for any given teacher's salary in California, X, is determined by:

`z=(X-\mu)/(\sigma)`

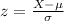
For X = $45,000:

`z=(45,000-37,764)/(5,100)\\ z=1.419`

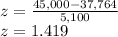
A z-score of 1.419 corresponds to the 92.20th percentile of a normal distribution. Therefore, the probability that a salary is greater than $45,000 is:

`P(X>\$45,000) = 1-0.9220\\P(X>\$45,000) = 0.078=7.8\%`

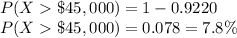
The probability is 0.078 or 7.8%.