Question

Consider a drug testing company that provides a test for marijuana usage. Among 317 tested​ subjects, results from 25 subjects were wrong​ (either a false positive or a false​negative). Use a 0.05 significance level to test the claim that less than 10 percent of the test results are wrong. Identify the null and alternative hypotheses for this test. Choose the correct answer below. A. Upper H 0H0​: pequals=0.10.1 Upper H 1H1​: pless than<0.10.1 B. Upper H 0H0​: pless than<0.10.1 Upper H 1H1​: pequals=0.10.1 C. Upper H 0H0​: pequals=0.10.1 Upper H 1H1​: pgreater than>0.10.1 D. Upper H 0H0​: pequals=0.10.1 Upper H 1H1​: pnot equals≠0.10.1 Identify the test statistic for this hypothesis test. The test statistic for this hypothesis test is nothing. ​(Round to two decimal places as​ needed.) Identify the​P-value for this hypothesis test. The​ P-value for this hypothesis test is nothing. ​(Round to three decimal places as​ needed.) Identify the conclusion for this hypothesis test. A. Fail to rejectFail to reject Upper H 0H0. There is notis not sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong. B. RejectReject Upper H 0H0. There is notis not sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong. C. RejectReject Upper H 0H0. There isis sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong. D. Fail to rejectFail to reject Upper H 0H0. There isis sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong. Click to select your answer(s).

Answer 1

The null and alternative hypothesis are:

`H_0: \pi=0.1\\\\H_a:\pi<0.1`

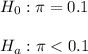
The test statistic for this hypothesis test is z=-1.15.

The​ P-value for this hypothesis test is P-value=0.124.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that less than 10 percent of the test results are wrong.

Explanation:

This is a hypothesis test for a proportion.

The claim is that less than 10 percent of the test results are wrong.

Then, the null and alternative hypothesis are:

`H_0: \pi=0.1\\\\H_a:\pi<0.1`

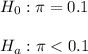
The significance level is 0.05.

The sample has a size n=317.

The sample proportion is p=0.079.

`p=X/n=25/317=0.079`

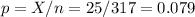
The standard error of the proportion is:

`\sigma_p=\sqrt{(\pi(1-\pi))/(n)}=\sqrt{(0.1*0.9)/(317)}\\\\\\ \sigma_p=√(0.000284)=0.017`

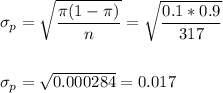
Then, we can calculate the z-statistic as:

`z=(p-\pi+0.5/n)/(\sigma_p)=(0.079-0.1+0.5/317)/(0.017)=(-0.019)/(0.017)=-1.153`

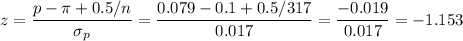
This test is a left-tailed test, so the P-value for this test is calculated as:

`P-value=P(z<-1.153)=0.124`

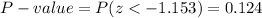
As the P-value (0.124) is greater than the significance level (0.05), the effect is not significant.

The null hypothesis failed to be rejected.

There is not enough evidence to support the claim that less than 10 percent of the test results are wrong.