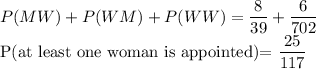Question

Suppose that two openings on an appellate court bench are to be filled from current municipal court judges. The municipal court judges consist of 24 men and 3 women. (Enter your probabilities as fractions.) (a) Find the probability that both appointees are men. (b) Find the probability that one man and one woman are appointed. (c) Find the probability that at least one woman is appointed.

Answer 1

`(a)(92)/(117)`

`(b)(8)/(39)`

`(c)(25)/(117)`

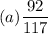
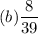
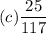
Explanation:

Number of Men, n(M)=24

Number of Women, n(W)=3

Total Sample, n(S)=24+3=27

Since you cannot appoint the same person twice, the probabilities are without replacement.

(a)Probability that both appointees are men.

`P(MM)=(24)/(27)X (23)/(26)=(552)/(702)\\=(92)/(117)`

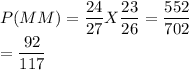
(b)Probability that one man and one woman are appointed.

To find the probability that one man and one woman are appointed, this could happen in two ways.

• A man is appointed first and a woman is appointed next.
• A woman is appointed first and a man is appointed next.

P(One man and one woman are appointed)
`=P(MW)+P(WM)`

`=((24)/(27)X (3)/(26))+((3)/(27)X (24)/(26))\\=(72)/(702)+(72)/(702)\\=(144)/(702)\\=(8)/(39)`

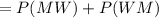
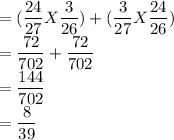
(c)Probability that at least one woman is appointed.

The probability that at least one woman is appointed can occur in three ways.

• A man is appointed first and a woman is appointed next.
• A woman is appointed first and a man is appointed next.
• Two women are appointed

P(at least one woman is appointed)
`=P(MW)+P(WM)+P(WW)`

`P(WW)=(3)/(27)X (2)/(26)=(6)/(702)`

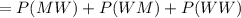
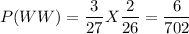
In Part B,
`P(MW)+P(WM)=(8)/(39)`

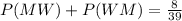
Therefore:

`P(MW)+P(WM)+P(WW)=(8)/(39)+(6)/(702)\\$P(at least one woman is appointed)=(25)/(117)`