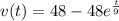Answer:
v(t) = 21.3t
v(t) = 5.3t
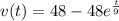
Step-by-step explanation:
When no sliding friction and no air resistance occurs:
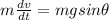
where;
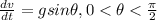
Taking m = 3 ; the differential equation is:
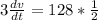
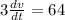
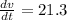
By Integration;
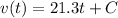
since v(0) = 0 ; Then C = 0
v(t) = 21.3t
ii)
When there is sliding friction but no air resistance ;
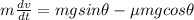
Taking m =3 ; the differential equation is;
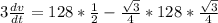
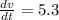
By integration; we have ;
v(t) = 5.3t
iii)
To find the differential equation for the velocity (t) of the box at time (t) with sliding friction and air resistance :
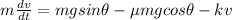
The differential equation is :
=

=
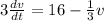
By integration
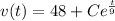
Since; V(0) = 0 ; Then C = -48