Question

Determine Z and V for steam at 250°C and 1800 kPa by the following: (a) The truncated virial equation [Eq. (3.38)] with the following experimental values of virial coefficients: B = −152.5 cm3·mol−1 C = −5800 cm6·mol−2 (b) The truncated virial equation [Eq. (3.36)], with a value of B from the generalized Pitzer correlation [Eqs. (3.58)–(3.62)]. (c) The steam tables (App. E).

Answer 1

Step-by-step explanation:

Given that:

the temperature
`T_1` = 250 °C= ( 250+ 273.15 ) K = 523.15 K

Pressure = 1800 kPa

a)

The truncated viral equation is expressed as:

`(PV)/(RT) = 1 + (B)/(V) + (C)/(V^2)`

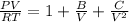
where; B = -
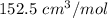`152.5 \ cm^3 /mol` C = -5800
`cm^6/mol^2`

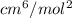
R = 8.314 × 10³ cm³ kPa. K⁻¹.mol⁻¹

Plugging all our values; we have

`(1800*V)/(8.314*10^3*523.15) = 1+ (-152.5)/(V) + (-5800)/(V^2)`

`4.138*10^(-4) \ V= 1+ (-152.5)/(V) + (-5800)/(V^2)`

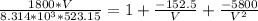
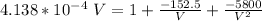
Multiplying through with V² ; we have

`4.138*10^4 \ V ^3 = V^2 - 152.5 V - 5800 = 0`

`4.138*10^4 \ V ^3 - V^2 + 152.5 V + 5800 = 0`

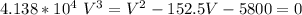
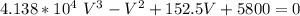
V = 2250.06 cm³ mol⁻¹

Z =
`(PV)/(RT)`

Z =
`(1800*2250.06)/(8.314*10^3*523.15)`

Z = 0.931

b) The truncated virial equation [Eq. (3.36)], with a value of B from the generalized Pitzer correlation [Eqs. (3.58)–(3.62)].

The generalized Pitzer correlation is :

`T_c = 647.1 \ K \\ \\ P_c = 22055 \ kPa \\ \\ \omega = 0.345`

`T__(\gamma)} = (T)/(T_c)`

`T__(\gamma)} = (523.15)/(647.1)`

`T__(\gamma)} = 0.808`

`P__(\gamma)} = (P)/(P_c)`

`P__(\gamma)} = (1800)/(22055)`

`P__(\gamma)} = 0.0816`

`B_o = 0.083 - (0.422)/(T__(\gamma))^(1.6)}`

`B_o = 0.083 - (0.422)/(0.808^(1.6))`

`B_o = 0.51`

`B_1 = 0.139 - (0.172)/(T__(\gamma))^( \ 4.2)}`

`B_1 = -0.282`

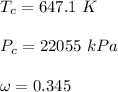
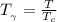
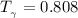
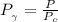
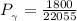
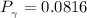
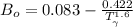
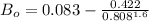
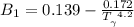
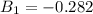
The compressibility is calculated as:

`Z = 1+ (B_o + \omega B_1 ) (P__(\gamma))/(T__(\gamma))`

`Z = 1+ (-0.51 +(0.345* - 0.282) ) (0.0816)/(0.808)`

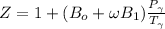
Z = 0.9386

`V= (ZRT)/(P)`

`V= (0.9386*8.314*10^3*523.15)/(1800)`

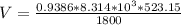
V = 2268.01 cm³ mol⁻¹

c) From the steam tables (App. E).

At
`T_1 = 523.15 \ K \ and \ P = 1800 \ k Pa`

V = 0.1249 m³/ kg

M (molecular weight) = 18.015 gm/mol

V = 0.1249 × 10³ × 18.015

V = 2250.07 cm³/mol⁻¹

R = 729.77 J/kg.K

Z =
`(PV)/(RT)`

Z =
`(1800*10^3 *0.1249)/(729.77*523.15)`

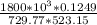
Z = 0.588