Question

A study of the effect of exposure to color (red or blue) on the ability to solve puzzles used 42 subjects. Half the subjects (21) were asked to solve a series of puzzles while in a red-colored environment. The other half were asked to solve the same series of puzzles while in a blue-colored environment. The time taken to solve the puzzles was recorded for each subject. The 21 subjects in the red-colored environment had a mean time for solving the puzzles of 9.64 seconds with standard deviation 3.43; the 21 subjects in the blue-colored environment had a mean time of 15.84 seconds with standard deviation 8.65.

The two-sample t statistic for comparing the population means has value _____ (± 0.001).

Answer 1

The two-sample t statistic for comparing the population means is -3.053.

Explanation:

We are given that the time taken to solve the puzzles was recorded for each subject.

The 21 subjects in the red-colored environment had a mean time for solving the puzzles of 9.64 seconds with standard deviation 3.43; the 21 subjects in the blue-colored environment had a mean time of 15.84 seconds with standard deviation 8.65.

Let
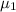`\mu_1` = average time taken to solve the puzzle in red-colored environment.

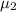`\mu_2` = average time taken to solve the puzzle in blue-colored environment.

So, Null Hypothesis,
`H_0` :
`\mu_1=\mu_2` {means that there is no difference in time taken to solve both the puzzles}

Alternate Hypothesis,
`H_A` :
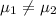`\mu_1\\eq \mu_2` {means that there is difference in time taken to solve both the puzzles}

The test statistics that would be used here Two-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p \sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t__n_1_-_n_2_-_2`

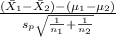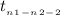
where,
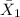`\bar X_1` = sample average time for solving the puzzles in the red-colored environment = 9.64 seconds

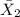`\bar X_2` = sample average time for solving the puzzles in the blue-colored environment = 15.84 seconds

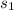`s_1` = sample standard deviation for red-colored environment = 3.43 seconds

`s_2` = sample standard deviation for blue-colored environment = 8.65 seconds

`n_1` = sample of subjects in the red-colored environment = 21

`n_2` = sample of subjects in the blue-colored environment = 21

Also,
`s_p=\sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
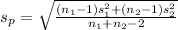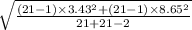`\sqrt{((21-1)* 3.43^(2)+(21-1)* 8.65^(2) )/(21+21-2) }` = 6.58

So, test statistics =
`\frac{(9.64-15.84)-(0)}{6.58 \sqrt{(1)/(21)+(1)/(21) } }` ~
`t_4_0`

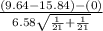= -3.053

The value of two-sample t test statistics is -3.053.