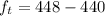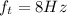Question

A musician on a unicycle is riding at a steady 6.2 m/s while playing their well tuned oboe at an A above middle C (440 Hz). They then ride toward another musician sitting on a park bench also playing an A above middle C. However it appears to them that one of them is off as they hear beats. If we assume both are tuned properly and the outside temperature is 27 oC what will the beat frequency they hear be

Answer 1

The frequency of the beat is
`f_t = 8Hz`

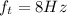
Step-by-step explanation:

From the question we are told that

The speed of the ride
`v = 6,2 m/s`

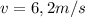
The frequency of the oboe is
`f = 440Hz`

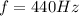
The temperature outside is
`T = 27^oC`

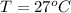
Generally the speed of sound generated in air is mathematically evaluated as

`v_s = 331 + 0.61 T`

Substituting value

`v_s = 331 + 0.61 *27`

`v_s = 347.47 \ m/s`

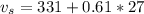
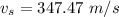
The frequency of sound(generated by the musician on he park) getting to the musicians on the unicycle is mathematically evaluated as

`f_a = (v_s )/(v_s - v) f`

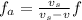
substituting values

`f_a = (347.47 )/(347.47 - 6.2) * 440`

`f_a = 448Hz`

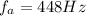
Since the musician on the park is not moving the frequency of sound (from the musicians riding the unicycle )getting to him is = 440Hz

The beat frequency these musician here is mathematically evaluated as

`f_t = f_a - f`

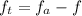
So
`f_t = 448 - 440`

`f_t = 8Hz`