Question

A very long, straight solenoid with a cross-sectional area of 2.16 cm^2 is wound with 85.7 turns of wire per centimeter. Starting at t = 0, the current in the solenoid is increasing according to i(t)= (( 0.175 A/s^2 )t^2). A secondary winding of 5 turns encircles the solenoid at its center, such that the secondary winding has the same cross-sectional area as the solenoid. What is the magnitude of the emf induced in the secondary winding at the instant that the current in the solenoid is 3.2A ?

Answer 1

1.74x10⁻⁵ V

Step-by-step explanation:

n = 85.7 turns/cm => 8570 turns/metre

The field inside the long solenoid is given by B = μ₀ni

B = 4πx10⁻⁷ x 8570 x 0.175t² = 1.884x10⁻³ t²

dB/dt = 3.78x10⁻³ t

Cross-sectional Area'A'= 2.16 cm²=> 2.16 x
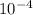`10^(-4)` m²

Now, rate of change of flux linkage '|Emf|' is given by:

|Emf| = d(NAB)/dt = NA dB/dt

|Emf| = 5 x 2.16 x
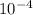`10^(-4)` x 3.78x10⁻³ t

|Emf| = 4.0824x10⁻⁶ t

Considering time 't' at which the current = 3.2A , we have

3.2 = 0.175T²

T² = 3.2/0.175

T = 4.28 s

|emf| = 4.0824x10⁻⁶ t => 4.0824x10⁻⁶ x4.28

|emf|= 1.74x10⁻⁵ V

Therefore,the magnitude of the emf induced in the secondary winding is 1.74x10⁻⁵ V