Answer:
z = 1.16m
Step-by-step explanation:
The electric field in a point of the axis of a charged ring, and perpendicular to the plane of the ring is given by:
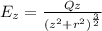
z: distance to the plane of the ring
r: radius of the ring
Q: charge of the ring
you have that:
E_{z->0} = 0
E_{z->∞} = 0
To find the value of z that maximizes E you use the derivative respect to z, and equals it to zero:
![(dE_z)/(dz)=Q[(1)/((z^2+r^2)^(3/2))+z(-(3)/(2))(1)/((z^2+r^2)^(5/2))(2z)]=0\\\\(z^2+r^2)^(5/2)=3z^2(z^2+r^2)^(3/2)\\\\(z^2+r^2)^2=3z^4\\\\z^4+2z^2r^2+r^4=3z^4\\\\2z^4-2z^2r^2-r^4=0\\\\z^2_(1,2)=(-(-2)+-√(4-4(2)(-1)))/(2(2))=(2\pm 3.464)/(4)\\\\](https://img.qammunity.org/2021/formulas/physics/college/s8v5o1poly2nk9siy1mi7a7m0yegi4h2kj.png)
you take the positive value:

hence, the distance in which the magnitude if the electric field is maximum is 1.16m