Question

A survey of 76 commercial airline flights of under 2 hours resulted in a sample average late time for a flight of 2.55 minutes. The population standard deviation was 12 minutes. Construct a 95% confidence interval for the average time that a commercial flight of under 2 hours is late. What is the point estimate? What does the interval tell about whether the average flight is late?

Answer 1

The best point of estimate for the true mean is:

`\hat \mu = \bar X = 2.55`

`2.55-1.96(12)/(√(76))=-0.148`

`2.55+1.96(12)/(√(76))=5.248`

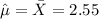
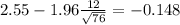
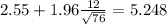
Since the time can't be negative a good approximation for the confidence interval would be (0,5.248) minutes. The interval are tellling to us that at 95% of confidence the average late time is lower than 5.248 minutes.

Explanation:

Information given

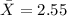`\bar X=2.55` represent the sample mean for the late time for a flight

`\mu` population mean

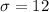`\sigma=12` represent the population deviation

n=76 represent the sample size

Confidence interval

The best point of estimate for the true mean is:

`\hat \mu = \bar X = 2.55`

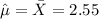
The confidence interval for the true mean is given by:

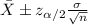`\bar X \pm z_(\alpha/2)(\sigma)/(√(n))` (1)

The Confidence level given is 0.95 or 95%, th significance would be
`\alpha=0.05` and
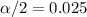`\alpha/2 =0.025`. If we look in the normal distribution a quantile that accumulates 0.025 of the area on each tail we got
`z_(\alpha/2)=1.96`

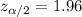
Replacing we got:

`2.55-1.96(12)/(√(76))=-0.148`

`2.55+1.96(12)/(√(76))=5.248`

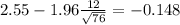
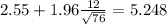
Since the time can't be negative a good approximation for the confidence interval would be (0,5.248) minutes. The interval are tellling to us that at 95% of confidence the average late time is lower than 5.248 minutes.