Question

In 2002, there were 972 students enrolled at Oakview High School. Since then, the number of students has increased by 1.5% each year. Write an exponential function to model the situation, then find the number of students enrolled in 2014. Is this considered growth or decay?

Answer 1

`N(t) = 972(1.015)^(t)`

Growth function.

The number of students enrolled in 2014 is 1162.

Explanation:

The number of students in the school in t years after 2002 can be modeled by the following function:

`N(t) = N(0)(1+r)^(t)`

In which N(0) is the number of students in 2002 and r is the rate of change.

If 1+r>1, the function is a growth function.

If 1-r<1, the function is a decay function.

In 2002, there were 972 students enrolled at Oakview High School.

This means that
`N(0) = 972`

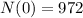
Since then, the number of students has increased by 1.5% each year.

Increase, so r is positive. This means that
`r = 0.015`

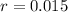
Then

`N(t) = N(0)(1+r)^(t)`

`N(t) = 972(1+0.015)^(t)`

`N(t) = 972(1.015)^(t)`

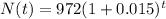
Growth function.

Find the number of students enrolled in 2014.

2014 is 2014-2002 = 12 years after 2002, so this is N(12).

`N(t) = 972(1.015)^(t)`

`N(12) = 972(1.015)^(12)`

`N(12) = 1162`

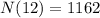
The number of students enrolled in 2014 is 1162.