Question

2. The value of C when y= 2x+C is tangent to the parabola y²=8x is: (a)-1 (b) 1 (c) 2 (d)-2​

Answer 1

B. The value of C is 1

Explanation:

Given:

`\displaystyle \large{y=2x+C}\\\displaystyle \large{y^2=8x}`

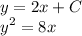
• y = 2x + C is a tangent to parabola y² = 8x

To find:

• value of C

A line being a tangent to curve means both equations are equal but there has to be only one interception between both graphs.

Therefore, substitute y = 2x+C in y² = 8x:

`\displaystyle \large{(2x+C)^2 =8x}`

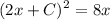
Expand the expression (2x+C)² using perfect square:

`\displaystyle \large{4x^2+4xC+C^2=8x}`

Simplify the equation:

`\displaystyle \large{4x^2+4xC-8x+C^2=0}\\\displaystyle \large{4x^2+(4C-8)x+C^2=0}`

The discriminant says:

• If b²-4ac > 0 then there are two real roots
• If b²-4ac = 0 then there is only one real root
• If b²-4ac < 0 then the are no real roots

For this, we choose b²-4ac = 0 since tangents only have one intersection.

`\displaystyle \large{b^2-4ac = (4C-8)^2-4(4)C^2 = 0}\\\displaystyle \large{16C^2-64C+64-16C^2=0}\\\displaystyle \large{-64C+64=0}`

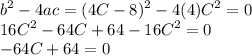
Solve the equation for C:

`\displaystyle \large{-64C=-64}\\\displaystyle \large{C=1}`

Therefore, the value of C is 1