Question

A polling organization had taken a survey of a sample of 200 people for one of their clients, in order to estimate a population percentage. Now the client would like them to reduce the margin of error by 50% (that is, the new margin of error should be half the original margin of error), while keeping the same level of confidence. To do this, how many people should they now survey

Answer 1

They now should survey 800 people.

Explanation:

In a sample with a number n of people surveyed with a probability of a success of
`\pi`, and a confidence level of
`1-\alpha`, we have the following confidence interval of proportions.

`\pi \pm z\sqrt{(\pi(1-\pi))/(n)}`

In which

z is the zscore that has a pvalue of
`1 - (\alpha)/(2)`.

The margin of error is:

`M = z\sqrt{(\pi(1-\pi))/(n)}`

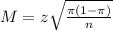
In this problem:

Same level of confidence, so same z

Same proportion, so same
`\pi`

We have to change n

We want to reduce the margin of error by half.

M is inverse proportion to the square root of n. That is, as n increases, M decreases.

We want to decrese M by half. So we need to increase n by a factor of 2^2 = 4

The first survey had a sample of 200 people

Increasing by a factor of 4.

200*4 = 800

They now should survey 800 people.