Answer:
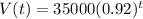
Decay function
The value of the car in 2015 is $19,525.
Explanation:
A exponential value function has the following format:
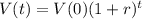
In which V(t) is the value after t years, V(0) is the initial value and 1+r is the yearly variation rate.
If 1+r>1, the function is a growth function.
If 1-r<1, the function is a decay function.
Mark bought a brand new car for $35,000 in 2008.
This means that
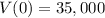
If the car depreciates in value approximately 8% each year
Depreciates, then r is negative. So

Then
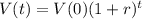

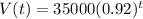
0.92 < 1, so decay function.
Then, find the value of the car in 2015.
2015 is 2015-2008 = 7 years after 2008. So this is V(7).
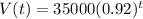
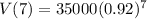

The value of the car in 2015 is $19,525.