Answer:
The work function is

Step-by-step explanation:
From the question we are told that
The wavelength of the green light is
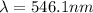
The stopping potential is
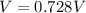
At stopping potential the kinetic is also maximum because this where the electron(causing the current ) would flow at it highest speed before return to zero
So the maximum kinetic energy of this electron in term of electron volt is

This maximum kinetic energy is mathematically represented as
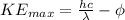
Where h is the planck's constant with a value

c is the speed of light

 is the work function
is the work function
Making
 the subject of the formula
the subject of the formula
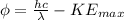
Substituting values

