Question

An 80-eV electron impinges upon a potential barrier 100 eV high and 0.20 nm thick. What is the probability the electron will tunnel through the barrier? (1 eV = 1.60 × 10-19 J, m proton = 1.67 × 10-27 kg, = 1.055 × 10-34 J · s, h = 6.626 × 10-34 J · s) a. 7.7 × 10-10 % b. 0.11% c. 1.1% d. 0.011% e. 1.1 × 10-4 %

Answer 1

d) 0.011%

Step-by-step explanation:

The probability for tunneling the barrier is given by the following formula:

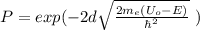`P=exp(-2d\sqrt{(2m_e(U_o-E))/(\hbar ^2) }\ )` ( 1 )

me: mass of the electron

Uo: energy of the barrier

E: energy of the electron

d: thickness of the barrier

By replacing the values of the parameters in (1), you obtain:

`P=exp(-2(0.20*10^(-9)m)\sqrt{(2(9.11*10^(-31)kg)(100eV-80eV)(1.60*10^(-19)J))/((1.055*10^(-34)Js)^2)})\\\\P=e^(-9.15)=1.08*10^(-4)\approx0.011\%`

hence, the probability is 0.011% (answer d)