Question

Philip shoots an arrow from the top of a hill into the ground. the flight of the arrow can be modeled with the quadratic function y=-5x^2+15x+90, where y represents the vertical height of the arrow, in meters, and x represents the time, in seconds. use factoring to find the positive zero of the function. what does this zero represent? then find the maximum value of the function by completing the square. what does the maximum value represent? explain each step in your answer.

Answer 1

(a)Time taken to reach the ground, x=6 seconds

(b)Maximum height of the arrow during its flight =101.25 feet

Explanation:

Given the quadratic function which models the flight of the arrow:

`y=-5x^2+15x+90`

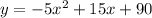
Where:

• y represents the vertical height of the arrow, in meters; and
• x represents the time, in seconds.

(a)Positive Zero

`-5x^2+15x+90=0\\-5(x^2-3x-18)=0\\-5(x^2-6x+3x-18)=0\\-5(x(x-6)+3(x-6))=0\\-5(x+3)(x-6)=0\\x+3=0\:or\:x-6=0\\x=-3,x=6`

In 6 seconds, the arrow will hit the horizontal plane, i.e. the ground.

(b)

`y=-5x^2+15x+90\\y-90=-5(x^2-3x)\\y-90-5((9)/(4)) =-5(x^2-3x+((3)/(2) )^2)\\y-101.25=-5(x-(3)/(2) )^2\\y=-5(x-(3)/(2) )^2+101.25`

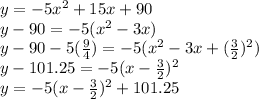
Comparing with the vertex form:

`y=a(x-h)^2+k`

Our vertex, (h,k)=(1.5, 101.25)

Maximum Value of y=101.25

The maximum value of y represents the maximum height of the arrow during its flight, which is 101.25 feet.