Question

The function f(x) = –x2 – 4x + 5 is shown on the graph. On a coordinate plane, a parabola opens down. It goes through (negative 5, 0), has a vertex at (negative 2, 9), and goes through (1, 0). Which statement about the function is true? The domain of the function is all real numbers less than or equal to −2. The domain of the function is all real numbers less than or equal to 9. The range of the function is all real numbers less than or equal to −2. The range of the function is all real numbers less than or equal to 9.

Answer 1

Zeros are (-5,0) and (1,0)

Hence

• y=-x²-4x+5
• y=-[x²+4x-5]
• y=-[x²+5x-x-5]
• y=-[x(x+5)-1(x+5)
• y=-(x-1)(x+5)

Yes this is the parabola given

• Convert to Vertex form a(x-h)²+k

So

• y=-[x²+4x-5]
• y=-[x²+2(2)(x)-5+9-9]
• y=-[x²+2(2x)+4-9]
• y=-[(x+2)²-9]
• y=-(x+2)²+9

As for any real x the function will give a real value [square present] the domain is set of real numbers ≤-2

vertex is maximum

Highest value of y is 9

Hence.

• range is ≤9

Or in interval notation

• range=(-oo,9]

Answer 2

The range of the function is all real numbers less than or equal to 9.

Explanation:

Given:

• 
  `f(x)=-x^2-4x+5`
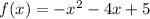
• vertex = (-2, 9)
• x-intercepts = (-5, 0) and (1, 0)

Domain: input values (x-values)

Range: output values (y-values)

The domain of the function is not restricted, so the domain is all real numbers.

The leading coefficient of the function is negative, therefore the parabola opens downwards. This means that the vertex is the maximum point.

Therefore, the range will be f(x) ≤ 9 → all real numbers less than or equal to 9.