Question

If the arc of a circle has length 10π and the circumference of the circle is 30π, what is the measure of the central angle that intercepts the arc?

Answer 1

We have been given that the arc of a circle has length 10π and the circumference of the circle is 30π. We are asked to find the measure of the central angle that intercepts the arc.

We will use arc length and circumference of circle formula to solve our given problem.

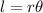`l=r\theta`, where,

l = Arc length,

r = radius,

`\theta` = Central angle that intercepts to arc.

`C=2\pi r`, where C represents circumference of circle.

We can solve for radius using circumference formula as:

`30\pi=2\pi r`

`(30\pi)/(2\pi)=(2\pi r)/(2\pi)`

`15=r`

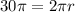
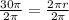
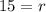
Upon substituting arc length and radius in arc length formula, we will get:

`10\pi =15\theta`

`(10\pi)/(15) =(15\theta)/(15)`

`(2\pi)/(3) =\theta`

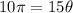
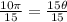
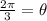
Therefore, the measure of central angle that intercepts the arc would be
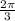`(2\pi)/(3)`.