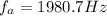Answer:
When they are approaching each other
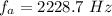
When they are passing each other

When they are retreating from each other
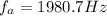
Step-by-step explanation:
From the question we are told that
The velocity of car one is
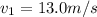
The velocity of car two is
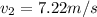
The frequency of sound from car one is

Generally the speed of sound at normal temperature is
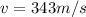
Now as the cars move relative to each other doppler effect is created and this can be represented mathematically as
![f_a = f_o [(v \pm v_o)/(v \pm v_s) ]](https://img.qammunity.org/2021/formulas/physics/college/g9jtjjyo9kqqzmustqsubnczovvwuylu82.png)
Where
 is the velocity of the source of sound
is the velocity of the source of sound
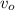 is the velocity of the observer of the sound
is the velocity of the observer of the sound
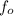 is the actual frequence
is the actual frequence
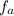 is the apparent frequency
is the apparent frequency
Considering the case when they are approaching each other
![f_a = f_o [(v + v_o)/(v - v_s) ]](https://img.qammunity.org/2021/formulas/physics/college/9cjqscsv8tnml3enx4t05h3csr25cei5nm.png)
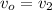
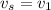
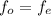
Substituting value
![f_a = 2100 [(343 + 7.22)/( 343 - 13) ]](https://img.qammunity.org/2021/formulas/physics/college/n1hl3llhvxmfwovnipdrdljwf5txa2wn2s.png)
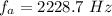
Considering the case when they are passing each other
At that instant
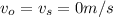
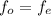
![f_a = f_o [(v )/(v ) ]](https://img.qammunity.org/2021/formulas/physics/college/rhmbcu74wg4l5cihjc1qvw53prng6jvk1v.png)

Substituting value

Considering the case when they are retreating from each other
![f_a = f_o [(v - v_o)/(v + v_s) ]](https://img.qammunity.org/2021/formulas/physics/college/riprk1bgsxq7xuepvfcpgpxxhpntdt5a9r.png)
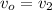
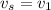
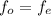
Substituting value
![f_a = 2100 [(343 - 7.22)/(343 + 13) ]](https://img.qammunity.org/2021/formulas/physics/college/ydnigmtkwk5x986q3oi3gwt89ptw1n8m68.png)