Question

Find the area of the rectangle polynomial​

Answer 1

hello,

`Area =(2x + 4) * ( 4x - 2) \\ Area =8 {x}^(2) - 4x + 16x - 8 \\ Area = {8x}^(2) + 12x - 8`

`\boxed{crsjr}`

Answer 2

`\Longrightarrow: \boxed{\sf{8x^2+12x-8}}`

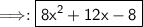
Explanation:

Using the distributive property, you multiply by the area to find the area of the rectangle polynomial.

`: \Longrightarrow \sf{(Area)= (2x+4)*(4x-2)}`

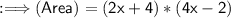
Solve.

(2x+4)*(4x-2)

Multiply by expand.

Use the distributive property.

Distributive property:

⇒ A(B+C)=AB+AC

Use the FOIL method.

FOIL method:

`\Longrightarrow: \sf{\left(A+B\right)\left(C+D\right)=AC+AD+BC+BD}`

`\Longrightarrow: \sf{2x\cdot \:4x+2x\left(-2\right)+4\cdot \:4x+4\left(-2\right)}`

`\Longrightarrow: \boxed{\sf{=8x^2+12x-8}}`

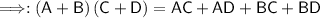
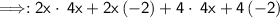
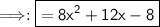
• Therefore, the correct answer is 8x²+12x-8.

I hope this helps! Let me know if you have any questions.