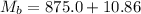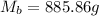Answer:
a
The tension in the string is
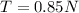
b
The new balance reading is
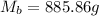
Step-by-step explanation:
From the question we are told that
The mass of the beaker of water is
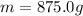
The diameter of the copper ball is
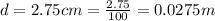
There are two forces acting on the copper ball
The first is the Buoyant force of the water pushing it up which is mathematically represented as
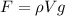
Where
 is the density of water which has value of
is the density of water which has value of
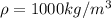
g is the acceleration due to gravity
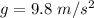
 is the volume of water displaced by the copper ball which is mathematically evaluated as
is the volume of water displaced by the copper ball which is mathematically evaluated as
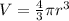
The radius r is
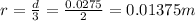
Substituting value

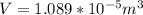
Substituting for F
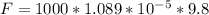
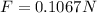
The second force is the weight of the copper ball which is mathematically represented as
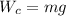
Now m is the mass which can be mathematically evaluated as
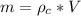
Where is the density of copper with value of
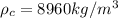
So
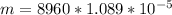
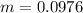
So the weight of copper is
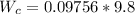
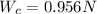
Now the tension the string would be mathematically evaluated as
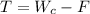
So
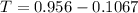
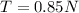
From this value we that the string is holding only 0.85 N of the copper weight thus (0.956 - 0.85 = 0.1065 N ) is being held by the balance
Now the mass equivalent of this weight is mathematically evaluated as


Converting to grams
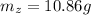
So the new balance reading is