Part A
A geometric sequence is where the terms increase by the same ratio.
Example:
7, 14, 28, 56, ...
We start at 7 and double each term to get the next term. The common ratio is 2.
============================================================
Part B
The next step is to subtract the two equations straight down. This will cancel the vast majority of the terms, and allow to solve for
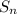 to get a fairly tidy formula. Refer to part C for more info.
to get a fairly tidy formula. Refer to part C for more info.
============================================================
Part C
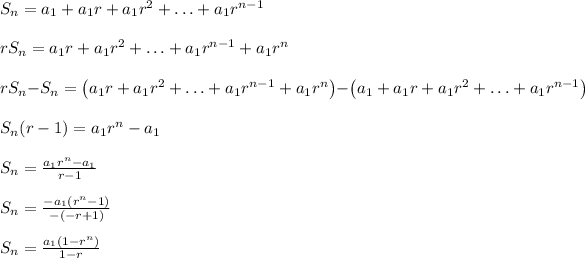
For more information about the canceling going on from step 3 to step 4, see the attachment below.