Question

Solve the right triangle. Round decimal answers to the nearest tenth.
AB= m

Answer 1

AB = 15

m<A = 53.1

m<B = 36.9

Explanation:

First use Pythagorean Theorem to solve for the missing side. The missing side is the hypothenuse so, we are looking to solve for c.

Your equation should look something like this:

`9^2 + 12^2 = c^2`

Solve for c

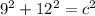
`9^2+12^2 = c^2\\81 + 144 = c^2\\225 = c^2\\√(225) = √(c)\\15 = c`

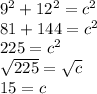
Line AB is of length 15.

Now, we just so happen to know that all triangles equal 180 degrees. We are given one of the angles, and we have some handy functions on our side to figure out the angles.

To get A, you can use either arcsin, arccos, arctan (or also known as
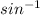`sin^(-1)`, etc.)

For now, I will just use sin which is opposite over hypothenuse.

The opposite of angle A is 12 and the hypothenuse is 15.

`sin^(-1)(12/15)`

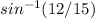
you will get approx. 53.13

So angle A is approx. 53.1

To get B, you do the same thing; you can use sin, cos, tan, whatever. It's your call. This time, I will use cos. No particular reason to choosing cos.

Cosine is adjacent (right beside) over hypothenuse. Adjacent of angle B is 12 and the hypothenuse is 15.

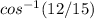`cos^(-1)(12/15)` will get you approx. 36.869

So angle B is approx. 36.9

To verify, the triangle must be 180 degrees. We can add up the angles together to verify our answer is correct.

So, 36.9 + 53.1 + 90 = 180!

If you do any problem and you verify and it does not equal 180 degrees, your answer is incorrect or the triangle is not a triangle (you will experience this later in High School).