Question

An article in the San Jose Mercury News stated that students in the California state university system take 4.5 years, on average, to finish their undergraduate degrees. Suppose you believe that the mean time is longer. You conduct a survey of 39 students and obtain a sample mean of 5.1 with a sample standard deviation of 1.2. Do the data support your claim at the 1% level?

Answer 1

We conclude that the mean time taken to finish undergraduate degrees is longer than 4.5 years.

Explanation:

We are given that an article in the San Jose Mercury News stated that students in the California state university system take 4.5 years, on average, to finish their undergraduate degrees.

You conduct a survey of 39 students and obtain a sample mean of 5.1 with a sample standard deviation of 1.2.

Let
`\mu` = average time taken to finish their undergraduate degrees.

So, Null Hypothesis,
`H_0` :
`\mu` = 4.5 years {means that the mean time taken to finish undergraduate degrees is equal to 4.5 years}

Alternate Hypothesis,
`H_A` :
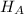`\mu` > 4.5 years {means that the mean time taken to finish undergraduate degrees is longer than 4.5 years}

The test statistics that would be used here One-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

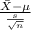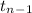
where,
`\bar X` = sample mean time = 5.1 years

s = sample standard deviation = 1.2 years

n = sample of students = 39

So, the test statistics =
`(5.1-4.5)/((1.2)/(√(39) ) )` ~
`t_3_8`

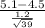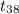
= 3.122

The value of t test statistics is 3.122.

Now, at 1% significance level the t table gives critical value of 2.429 at 38 degree of freedom for right-tailed test.

Since our test statistic is more than the critical value of t as 3.122 > 2.429, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the mean time taken to finish undergraduate degrees is longer than 4.5 years.