Answer:
The size of the sample should be at least 1037.
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence level of
, and a confidence level of
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of
 .
.
The margin of error of the interval is given by:
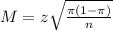
99% confidence level
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
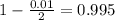 , so
, so
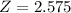 .
.
A level of confidence of 99% will be used and an error of no more than .04 is desired. There is no knowledge as to what the population proportion will be. The size of sample should be at least
We need a sample size of at least n.
n is found when
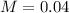
We don't know the proportion of the population, so we use

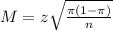
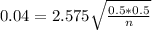
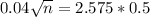
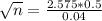
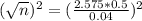
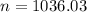
Rounding up
The size of the sample should be at least 1037.