Question

A bus travels on an east-west highway connecting two cities A and B that are 100 miles apart. There are 2 services stations along the route. The first service station is located 20 miles from city A, and the second service station is located 30 miles from city B. If the bus breaks down at a random point along the route, find the expected value of the distance of the bus from the nearest service station.

Answer 1

51/4

Explanation:

To begin with you have to understand what is the distribution of the random variable. If X represents the point where the bus breaks down. That is correct.

X~ Uniform(0,100)

Then the probability mass function is given as follows.

`f(x) = P(X=x) = 1/100 \,\,\,\, \text{if} \,\,\,\, 0 \leq x \leq 100\\f(x) = P(X=x) = 0 \,\,\,\, \text{otherwise}`

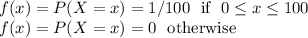
Now, imagine that the D represents the distance from the break down point to the nearest station. Think about this, the first service station is 20 meters away from city A, and the second station is located 70 meters away from city A then the mid point between 20 and 70 is (70+20)/2 = 45 then we can represent D as follows

`D(x) =\left\{ \begin{array}{ll} x & \mbox{if } 0\leq x \leq 20 \\ x-20 & \mbox{if } 20\leq x < 45\\ 70-x & \mbox{if } 45 \leq x \leq 70\\ x-70 & \mbox{if } 70 \leq x \leq 100\\ \end{array}\right.`

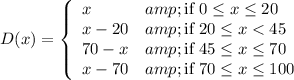
Now, as we said before X represents the random variable where the bus breaks down, then we form a new random variable
`Y = D(X)`,
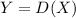`Y` is a random variable as well, remember that there is a theorem that says that

`E[Y] = E[D(X)] = \int\limits_(-\infty)^(\infty) D(x) f(x) \,\, dx`

Where
`f(x)` is the probability mass function of X. Using the information of our problem

`E[Y] = \int\limits_(-\infty)^(\infty) D(x)f(x) dx \\= (1)/(100) \bigg[ \int\limits_(0)^(20) x dx +\int\limits_(20)^(45) (x-20) dx +\int\limits_(45)^(70) (70-x) dx +\int\limits_(70)^(100) (x-70) dx \bigg]\\= (51)/(4) = 12.75`