Question

Historically, a certain region has experienced 92 thunder days annually. (A "thunder day" is day on which at least one instance of thunder is audible to a normal human ear). Over the past fifteen years, the mean number of thunder days is 72 with a standard deviation of 38. Can you conclude that the mean number of thunder days is less than 92? Use the level of significance.

Answer 1

We conclude that the mean number of thunder days is less than 92.

Explanation:

We are given that Historically, a certain region has experienced 92 thunder days annually.

Over the past fifteen years, the mean number of thunder days is 72 with a standard deviation of 38.

Let
`\mu` = mean number of thunder days.

So, Null Hypothesis,
`H_0` :
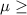`\mu \geq` 92 days {means that the mean number of thunder days is more than or equal to 92}

Alternate Hypothesis,
`H_A` :
`\mu` < 92 days {means that the mean number of thunder days is less than 92}

The test statistics that would be used here One-sample t test statistics as we don't know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

where,
`\bar X` = sample mean number of thunder days = 72

s = sample standard deviation = 38

n = sample of years = 15

So, test statistics =
`(72-92)/((38)/(√(15) ) )` ~
`t_1_4`

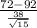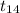
= -2.038

The value of z test statistics is -2.038.

Since, in the question we are not given with the level of significance so we assume it to be 5%. Now, at 5% significance level the t table gives critical value of -1.761 at 14 degree of freedom for left-tailed test.

Since our test statistics is less than the critical value of t as -2.038 < -1.761, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the mean number of thunder days is less than 92.