Question

Multiple-Concept Example 7 and Interactive LearningWare 26.1 provide some helpful background for this problem. The drawing shows a crystalline slab (refractive index 1.665) with a rectangular cross section. A ray of light strikes the slab at an incident angle of 1 = 37.0°, enters the slab, and travels to point P. This slab is surrounded by a fluid with a refractive index n. What is the maximum value of n such that total internal reflection occurs at point P?

Answer 1

n = 1.4266

Step-by-step explanation:

Given that:

refractive index of crystalline slab n = 1.665

let refractive index of fluid is n.

angle of incidence θ₁ = 37.0°

Critical angle
`\theta _c = sin^(-1) ((n)/(n_(slab)) )`

`sin \theta _ c =(n)/(n_(slab))`

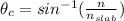
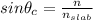
According to Snell's law of refraction:

`n sin \theta _1 = n_(slab) \ sin \ (90- \theta_c)`

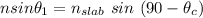
At point P ;
`90 - \theta _2 \leq \theta _c`

`\theta _2 = 90 - \theta _c`

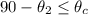
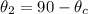
Therefore:

`n \ sin \theta_1 = n_(slab) √((1-sin^2 \theta _c)) \\ \\ n \ sin \theta_1 = n_(slab) \sqrt{(1- (n)/(n_(slab)) )}`

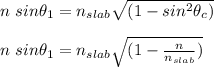
Then maximum value of refractive index n of the fluid is:

`n = (n_(slab))/(√(1+ sin^2 \theta _1 ) )`

`n = (1.665)/(√(1+ sin^2 \ 37) )`

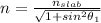
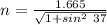
n = 1.4266