Answer:
95% confidence interval for the difference in population proportions of couples with children and with no children is [0.00134 , 0.219].
Explanation:
We are given that an aquarium manager wants to study gift shop browsing.
She randomly observes 120 couples that visit the aquarium with children and finds that 107 enter the gift shop at the end of their visit. She randomly observes 76 couples that visit the aquarium with no children and finds that 59 enter the gift shop at the end of their visit.
Firstly, the pivotal quantity for 95% confidence interval for the difference between population proportions is given by;
P.Q. =
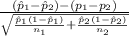 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of couples that visit the aquarium with children who enters the gift shop at the end of their visit =
= sample proportion of couples that visit the aquarium with children who enters the gift shop at the end of their visit =
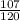 = 0.89
= 0.89
 = sample proportion of couples that visit the aquarium with no children who enters the gift shop at the end of their visit =
= sample proportion of couples that visit the aquarium with no children who enters the gift shop at the end of their visit =
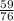 = 0.78
= 0.78
 = sample of couples that visit the aquarium with children = 120
= sample of couples that visit the aquarium with children = 120
 = sample of couples that visit the aquarium with no children = 76
= sample of couples that visit the aquarium with no children = 76
Here for constructing 95% confidence interval we have used Two-sample z proportion statistics.
So, 95% confidence interval for the difference between population proportions, is ;
P(-1.96 < N(0,1) < 1.96) = 0.95 {As the critical value of z at 2.5% level
of significance are -1.96 & 1.96}
P(-1.96 <
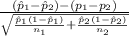 < 1.96) = 0.95
< 1.96) = 0.95
P(
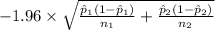 <
<
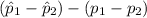 <
<
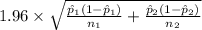 ) = 0.95
) = 0.95
P(
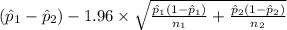 <
<
 <
<
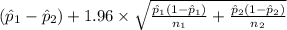 ) = 0.95
) = 0.95
95% confidence interval for
 =
=
[
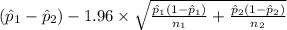 ,
,
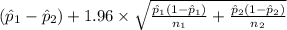 ]
]
= [
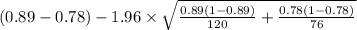 ,
,
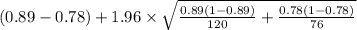 ]
]
= [0.00134 , 0.219]
Therefore, 95% confidence interval for the difference in population proportions of couples with children and with no children is [0.00134 , 0.219].