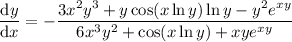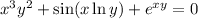
Differentiate both sides, treating
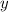 as a function of
as a function of
 . Let's take it one term at a time.
. Let's take it one term at a time.
Power, product and chain rules:
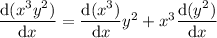
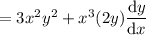
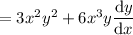
Product and chain rules:
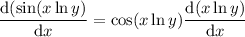
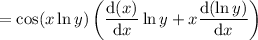
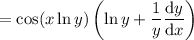
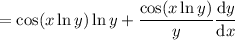
Product and chain rules:
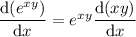
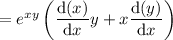
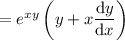
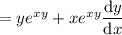
The derivative of 0 is, of course, 0. So we have, upon differentiating everything,
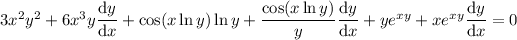
Isolate the derivative, and solve for it:
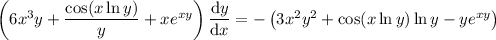
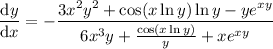
(See comment below; all the 6s should be 2s)
We can simplify this a bit by multiplying the numerator and denominator by
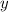 to get rid of that fraction in the denominator.
to get rid of that fraction in the denominator.