Question

Consider a drug testing company that provides a test for marijuana usage. Among 317 tested​ subjects, results from 25 subjects were wrong​ (either a false positive or a false​negative). Use a 0.05 significance level to test the claim that less than 10 percent of the test results are wrong. Identify the null and alternative hypotheses for this test. Choose the correct answer below. A. Upper H 0H0​: pequals=0.10.1 Upper H 1H1​: pless than<0.10.1 B. Upper H 0H0​: pless than<0.10.1 Upper H 1H1​: pequals=0.10.1 C. Upper H 0H0​: pequals=0.10.1 Upper H 1H1​: pgreater than>0.10.1 D. Upper H 0H0​: pequals=0.10.1 Upper H 1H1​: pnot equals≠0.10.1 Identify the test statistic for this hypothesis test. The test statistic for this hypothesis test is nothing. ​(Round to two decimal places as​ needed.) Identify the​P-value for this hypothesis test. The​ P-value for this hypothesis test is nothing. ​(Round to three decimal places as​ needed.) Identify the conclusion for this hypothesis test. A. Fail to rejectFail to reject Upper H 0H0. There is notis not sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong. B. RejectReject Upper H 0H0. There is notis not sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong. C. RejectReject Upper H 0H0. There isis sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong. D. Fail to rejectFail to reject Upper H 0H0. There isis sufficient evidence to warrant support of the claim that less than 1010 percent of the test results are wrong.

Answer 1

We conclude that we fail to reject
`H_0` as there is not sufficient evidence to warrant support of the claim that less than 10 percent of the test results are wrong.

Explanation:

We are given that among 317 tested​ subjects, results from 25 subjects were wrong.

We have to test the claim that less than 10 percent of the test results are wrong.

Let p = proportion of subjects that were wrong.

So, Null Hypothesis,
`H_0` : p = 10% {means that 10 percent of the test results are wrong}

Alternate Hypothesis,
`H_A` : p < 10% {means that less than 10 percent of the test results are wrong}

The test statistics that would be used here One-sample z proportion statistics;

T.S. =
`\frac{\hat p-p}{\sqrt{(\hat p (1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of test results that were wrong =
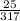`(25)/(317)` = 0.08

n = sample of tested subjects = 317

So, test statistics =
`\frac{0.08-0.10}{\sqrt{(0.08 (1-0.08))/(317) } }`

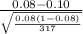
= -1.31

The value of z test statistics is -1.31.

Now, the P-value of the test statistics is given by the following formula;

P-value = P(Z < -1.31) = 1 - P(Z
`\leq` 1.31)

= 1 - 0.9049 = 0.095

Now, at 0.05 significance level the z table gives critical value of -1.645 for left-tailed test. Since our test statistics is more than the critical value of z as -1.31 > -1.645, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that we fail to reject
`H_0` as there is not sufficient evidence to warrant support of the claim that less than 10 percent of the test results are wrong.