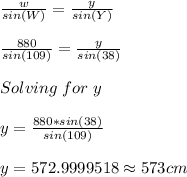Question

In ΔWXY, w = 880 cm, ∠X=33° and ∠Y=38°. Find the length of y, to the nearest centimeter.

Answer 1

573 cm

Explanation:

Answer 2

`y\approx573cm`

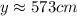
Explanation:

First, take a look to the picture that I attached, however please note the triangle is not drawn to scale, the figure is just to provide visual aid. As you can see the value of
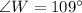`\angle W =109^(\circ)` this is because of the sum of the interior angles in a triangle is always equal to 180°. So:

`\angle W + \angle X + \angle Y =180\\\\\angle W = 180- \angle X -\angle Y\\\\\angle W =180-38-33\\\\\angle W=109`

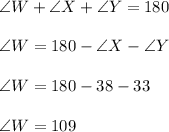
Now, we can use the law of sines, which states:

`(w)/(sin(W)) =(x)/(sin(X)) =(y)/(sin(Y))`

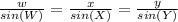
Hence:

`(w)/(sin(W)) =(y)/(sin(Y))\\\\(880)/(sin(109)) =(y)/(sin(38))\\\\Solving\hspace{3}for\hspace{3}y\\\\y=(880*sin(38))/(sin(109)) \\\\y=572.9999518\approx 573 cm`