Answer:
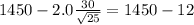
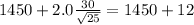
And the best option would be:
c. 1450 +/- 12
Explanation:
Information provided
 represent the sample mean for the SAT scores
represent the sample mean for the SAT scores
 population mean (variable of interest)
population mean (variable of interest)
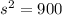 represent the sample variance given
represent the sample variance given
n=25 represent the sample size
Solution
The confidence interval for the true mean is given by :
 (1)
(1)
The sample deviation would be
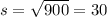
The degrees of freedom are given by:
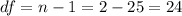
The Confidence is 0.954 or 95.4%, the value of
 and
and
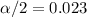 , assuming that we can use the normal distribution in order to find the quantile the critical value would be
, assuming that we can use the normal distribution in order to find the quantile the critical value would be
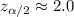
The confidence interval would be
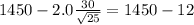
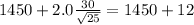
And the best option would be:
c. 1450 +/- 12