Answer:
![\sqrt[n]{x^m}=x^{(m)/(n)}](https://img.qammunity.org/2021/formulas/mathematics/college/mjxwn6k3p3g9rh9voauwg15zjjbyyqzcem.png)
Explanation:
A radical represents a fractional power. For example, ...
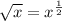
This makes sense in view of the rules of exponents for multiplication.
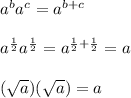
So, a root other than a square root can be similarly represented by a fractional exponent.
____
The power of a radical and the radical of a power are the same thing. That is, it doesn't matter whether the power is outside or inside the radical.
![\sqrt[n]{x^m}=x^{(m)/(n)}=(\sqrt[n]{x})^m](https://img.qammunity.org/2021/formulas/mathematics/college/vakm1ojsejvd7b6j52j4p5v4gpu1lwc50z.png)