Answer:
2.83m
Step-by-step explanation:
The information that we have is
Intensity at 2.0 m:
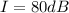 and
and
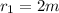
we need an intensity level of:
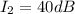
thus, we are looking for the distance
 .
.
which we can find with the law for intensity and distance:
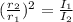
we solve for
 :
:
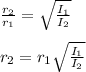
and we substitute the known values:
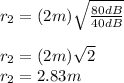
at a distance of 2.83m the intensity level is 40dB