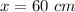Question

A uniform meter stick is pivoted at the 50.00 cm mark on the meter stick. A 400.0 gram object is hung at the 20.0 cm mark on the stick and a 320.0 gram object is hung at the 75.0 cm mark. Drawing is approximate. The meter stick is unbalanced. Determine the cm-mark on the meterstick that a 400 gram object needs to be hung to achieve equilibrium. A) 10.0 B) 40.0 C) 60.0 D) 90.0 E) none of the above is within 10% of my answer

Answer 1

Answer:C

Step-by-step explanation:

Given

mass
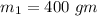`m_1=400\ gm` is at
`x=20\ cm` mark

mass
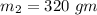`m_2=320\ gm` is at
`x=75\ cm` mark

Scale is Pivoted at
`x=50\ cm mark`

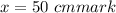
For scale to be in equilibrium net torque must be equal to zero

Taking ACW as positive thus

`T_(net)=0.4* g* (0.5-0.2)-0.32* g*(0.75-0.50)`

`T_(net)=0.12g-0.08g=0.04g`

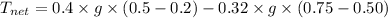
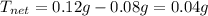
Therefore a net torque of 0.04 g is required in CW sense which a mass
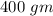`400\ gm` can provide at a distance of
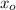`x_o` from pivot

`0.04g=0.4* g* x_o`

`x_o=0.1\ m`

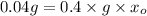
therefore in meter stick it is at a distance of
`x=60\ cm`