Question

A four-cylinder, four-stroke spark-ignition engine operates at 2800 RPM. The processes within each cylinder can be modeled as an air-standard Otto cycle with a temperature of 280 K and a pressure of 70 kPa at the beginning of the compression process. The compression ratio is 10, and the total engine volume is 2555.6 cm3 . Suppose heat generated from the combustion process (i.e. heat addition per unit mass) is 1080 kJ/kg and air is an ideal gas having variable specific heats. Determine: (a) Total mass of air in the engine (in kg) (6 Points) (b) Determine the power developed by the engine (in hp). (24 Points)

Answer 1

a) Total mass of air in the engine (in kg) = 0.00223 kg

b) power developed by the engine (in hp) = 180.61 hp

Step-by-step explanation:

Initial temperature,
`T_(1) = 280 K\\`

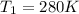
Initial pressure,
`P_(1) = 70 kPa`

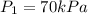
Compression ratio, r = 10

The initial total engine volume,
`V_(1) = 2555.6 cm^(3) = 2555.6 * 10^(-6) m^(3)`

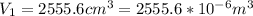
a) Total mass of air in the engine

Using the gas equation,
`P_(1) V_(1) = mRT_(1)`

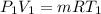
Where R = 0.287 kJ/kg-K

70 * 2555.6 * 10⁻⁶ = m * 0.287 * 280

`m = (70 * 2555.5 * 10^(-6) )/(0.287 * 280)`

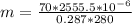
m = 0.00223 kg

b) Power developed by the engine

Heat generated due to combustion,
`Q_(in) = 1080 kJ/kg`

`(T_(2) )/(T_(1) )= ((V_(1) )/(V_(2) ))^(\gamma -1)`

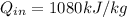
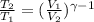
Compression ratio,
`r = (V_(2) )/(V_(1) ) = 10`

`(T_(2) )/(T_(1) )=10^(0.4)\\(T_(2) )/(280 )=10^(0.4)\\T_(2) = 280 * 10^(0.4)\\T_(2) = 703.328 K`

`Q_(in) = c_(v) (T_(3) -T_(2) )`

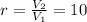
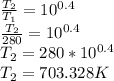
Where Specific capacity of air,
`c_(v) = 0.718 kJ/kg-K`

`1080 = 0.718 (T_(3) -703.328 )\\1504.18 + 703.328 = T_(3)\\ T_(3) = 2207.51 K`

`(T_(4) )/(T_(3) ) = ((V_(2) )/(V_(1) ) )^(\gamma -1) \\(T_(4) )/(T_(3) ) = (1/10 )^(0.4) \\(T_(4) )/(2207.51 ) = (1/10 )^(0.4) \\T_(4) = 2207.51 * (1/10 )^(0.4) \\T_(4) = 878.82 K`

`Q_(out) = c_(v) (T_(4) - T_(1) )\\Q_(out) = 0.718 (878.82 - 280 )\\Q_(out) = 430 kJ/kg`

`w_(net) = Q_(in) - Q_(out)\\w_(net) = 1080 - 430\\w_(net) = 650 kJ/kg`

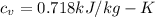
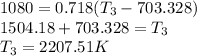
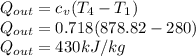
There are 4 cylinders, k = 4

N = 2800/2

N = 1400

Power developed by the engine,

`P =( mw_(net) Nk)/(60) \\P =( 0.00223*650* 1400*4)/(60) \\P = 134.68 kW`

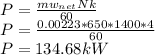
1 kW = 1.34102 hp

P = 134.68 * 1.34102

P = 180.61 hp