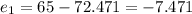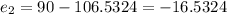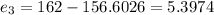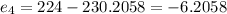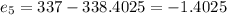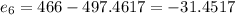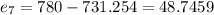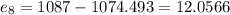Answer:
Predicted values:
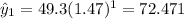
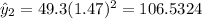
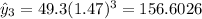
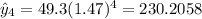
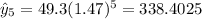
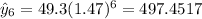
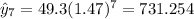
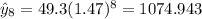
Residuals:
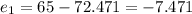
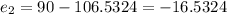
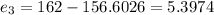
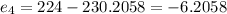
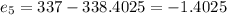
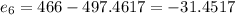
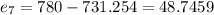
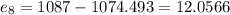
Explanation:
For this case we assume the following exponential function:
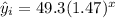
Where x represent the hours and y the predicted values for each hour. We can find the estimated values like this:
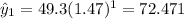
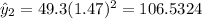
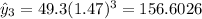
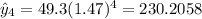
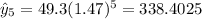
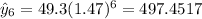
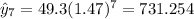
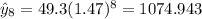
Now we can find the residuals with this formula:
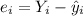
And replacing we got: