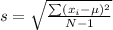Question

Which formula is used to calculate the standard deviation of sample data?

cok
n-1
100. ()*(3*3)*==(x-)
0 /6 -> * (37)*(
n-1

Answer 1

`s=\sqrt{(\sum (x_(i) -\mu)^(2) )/(N-1) }`

Explanation:

In statistics, the standard deviation is a measure about the amount of variation of a dataset.

The variation is measured through comparison between each data and the mean of the dataset. This way, we could get a numerical information about how far are those values form the mean (which represents the central value).

The formula to find the standard deviation of a sample is

`s=\sqrt{(\sum (x_(i) -\mu)^(2) )/(N-1) }`

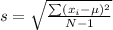
Where
`\mu` is the sample mean and
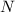`N` is the total number of values there are.

In the formula you can notice the difference between each value (
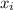`x_(i)`) and the mean (
`\mu`), That's why the standard deviation is commonly use to measure variation.

Therefore, the answer is

`s=\sqrt{(\sum (x_(i) -\mu)^(2) )/(N-1) }`