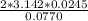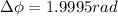Question

Two loudspeakers are placed on a wall 2 m apart. A listener stands directly in front of one of the speakers, 81.7 m from the wall. The speakers are being driven by the same electric signal generated by a harmonic oscillator of frequency 4450 Hz. What is the phase difference ∆Φ between the two waves (generated by each speaker) when they reach the listener? The speed of the sound in air is 343 m/s. Answer in units of rad.

Answer 1

The phase difference is
`\Delta \phi = 1.9995 rad`

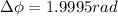
Step-by-step explanation:

From the question we are told that

The distance between the loudspeakers is
`d = 2m`

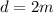
The distance of the listener from the wall
`D = 81.7 \ m`

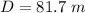
The frequency of the loudspeakers is
`f = 4450Hz`

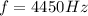
The velocity of sound is
`v_s = 343 m/s`

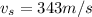
The path difference of the sound wave that is getting to the listener is mathematically represented as

`\Delta z =√(d^2 + D^2) -D`

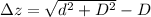
Substituting values

`\Delta z =√(2^2 + 81.7^2 ) -81.7`

`\Delta z =0.0245m`

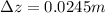
The phase difference is mathematically represented as

`\Delta \phi` =
`(2 \pi)/(\lambda ) * \Delta z`

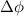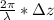
Where
`\lambda` is the wavelength which is mathematically represented as

`\lambda = (v_s )/(f)`

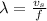
substituting value

`\lambda = (343 )/(4450)`

`\lambda = 0.0770 m`

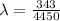
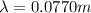
Substituting value into the equation for phase difference

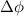`\Delta \phi` =
`(2 * 3.142 * 0.0245)/(0.0770)`

`\Delta \phi = 1.9995 rad`