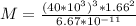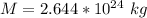Answer:
The mass of the star would be
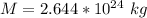
Step-by-step explanation:
From the question we are told that
The angular speed is

The radius of the star is
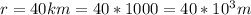
Generally the minimum mass of the start is mathematically evaluated as
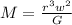
Where is the gravitational constant with a values of