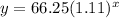Question

Write an exponential model, y=a(b)^x, given the two points (9,171) and (10,190)

Please hurry!

Answer 1

y = 66.25[(10/9)^x]

Explanation:

171 = a(b⁹)

b⁹ = 171/a

190 = a(b¹⁰)

190 = a(171/a) × b

b = 190/171

b = 10/9

(10/9)⁹ = 171/a

a = 66.24890362

Answer 2

`y = 66.25(1.11)^x`

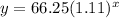
Explanation:

Let's plug in 9 for x and 171 for y into the given exponential equation:

y =
`ab^x`

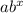
171 =
`ab^9`

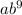
Now do the same with (10, 190):

190 =
`ab^(10)`

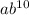
Write them both in terms of a and set them equal:

a = 171/
`b^9`

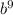
a = 190/
`b^(10)`

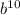
171/
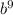`b^9` = 190/
`b^(10)`

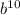
Multiply both sides by
`b^(10)`:

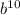171b = 190

b = 190/171 = 10/9 ≈ 1.11

Plug this in to find a:

a = 171 / (10/9)^9 ≈ 66.25

So, the exponential model is:

`y = 66.25(1.11)^x`